Analysis Statistics

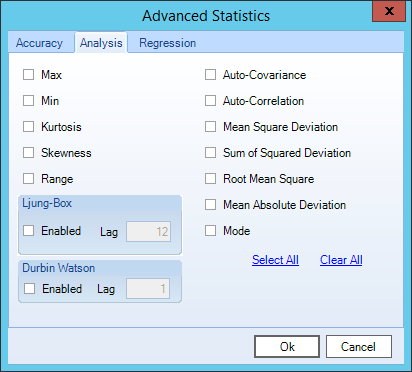
This section details the statistics that can be found under in the Analysis area of the Statistics tab, as well as the Analysis tab after clicking More Statistics.

Durbin Watson

When measuring accuracy, it is necessary to test for auto-correlation within the errors. Auto-correlation occurs when there is dependence between the successive error values, which is also called a serial correlation.

Durbin Watson is the most widely used statistic to determine random errors. The Durbin Watson statistic always lies between 0 and 4. If it is closer to zero, it indicates a positive auto-correlation. A value close to 4 indicates negative auto-correlation. A value close to 2 tends to reinforce the conclusion that no correlation exists among the error.

Therefore, values below 2 represent positive serial correlation amongst the errors, and values above 2 represent negative serial correlation amongst the errors.

Mean

The mean of a group of numbers is synonymous with the average. It is calculated by summing up the values of the items and then dividing the total by the number of items summed. Like the median, it is often used as a measure of location for a frequency or probability distribution.

Median

The median of a sequence of items is the middle item after the entire sequence is arranged in either ascending or descending order. This is often used to measure the location for a frequency or probability distribution.

Standard Deviation

The standard deviation is a descriptive statistic which is derived from taking the square root of the variance. The variance allows us to see how far each data point is from the average point (mean) in the data set.

Variance

The variance is a descriptive statistic that measures the dispersion of the data. Variance is calculated by finding out how far each data point is from the mean.

Mean Square Deviation

The Sum Squared Deviations (SS) is divided by the degrees of freedom associated with it to obtain the Mean Squared Deviation (MS). The sample variance is often called a mean square because a sum of squares has been divided by the appropriate degrees of freedom.

Correlation Coefficient

The correlation coefficient tells how strongly two variables are related. The value of the correlation coefficient is always between -1 and 1. That means that if the value is 0, then the two variables (X and Y) are independent. If the correlation coefficient is positive, it means when X is large, Y is likely to be large also.

If the correlation coefficient is closer to 1, then X and Y are almost directly related. However, if there is a negative correlation, it means when X is large, Y is likely to be small. The closer the correlation coefficient is to -1, the stronger the negative correlation.

Max

Max (maximum) is the largest value in your data set.

Min

Min (minimum) is the smallest value in your data set.

Kurtosis

The Kurtosis of a distribution measures the thickness of the tails of a distribution. See Skewness on page 121. Kurtosis is a measure of flatness and tail thickness of a distribution, as compared with the normal distribution.

Positive kurtosis, or leptokurtic, indicates a relatively peaked distribution. Negative kurtosis, or platykurtic, indicates a relatively flat distribution. For a normal distribution, kurtosis is equal to 3. When the tail of the distribution is thicker than the normal distribution, kurtosis will be greater than 3. When the tail of the distribution is thinner than the normal distribution, the kurtosis will be less than 3.

Skewness

Like mean and variance, which calculating the distribution of a random variable, the skewness of a distribution measures whether the distribution is symmetrical. Asymmetric distribution has a skewness of 0. If the tail of the distribution is long and in the positive direction, then it has positive skewness. If the distribution has a long tail in the negative direction, then the skewness is negative.

Range

The range is the difference between the max and the min.

Auto-Covariance

Auto-Covariance is a measure in a single time series of the linear relationship between two data points separated by a constant time interval or specified number of lags. Auto-Covariance shows whether time-related patterns exist within a given time series.

Auto-Correlation

Auto-correlation describes the dependence between two variables of the same time series at different time periods. Auto-correlation helps determine if there is a causal connection between two variables even though there is a time lag between their occurrences. For example, auto-correlation can be useful in sales for determining if a special promotional event occurring at regular intervals is a causal factor in increased sales after the events happen. Auto-correlation answers the question, "Even though X happens with Y, is Y dependent on X?"

Not only can auto-correlation be used to determine seasonality, it also helps describe if a series is stationary. A stationary series is one that has properties independent of the time period in which they occurred.

Coefficient of Variation

The relative amount of dispersion in the data can be calculated by expressing the standard deviation as a percentage of the mean. This measurement is called the Coefficient of Variation. This allows comparison of the dispersions of two separate data sets that are entirely different.

Sum of Squared Deviation

Given a single data series, each observation is subtracted from the estimated mean of the data series and then squared. All observations are then summed to produce the Sum Squared Deviations. The Sum Squared Deviations are used to calculate the sample variance, alternatively called the Mean Squared Deviation (MS), of a single data series.

Root Mean Square

The Root Mean Square error is a measure of the deviation of the forecasted value from the actual value. In Root Mean Square, the deviations are summed and then divided by the number of time periods in the time series. Lastly, the square root of this quantity is evaluated. The Root Mean Square is used to quantitatively measure how closely the forecasted variable tracks the actual data. The magnitude of the Root Mean Square error can be evaluated only by comparing it to the mean of the time series.

Mean Absolute Deviation

The Mean Absolute Deviation is the mean of the absolute value of the differences between the supplied values and the arithmetic mean of all values. The formula for Mean Absolute Deviation is:

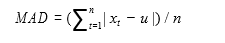
The variables used in Mean Absolute Deviation are defined as follows: n=the number of values; x=the supplies values; µ=the arithmetic mean of all the values.

Mode

Mode is the value or values that appear most frequently within your data set.

Ljung Box

Ljung Box tests for the overall correlation of the fitted errors of a model. It determines how a variable relates to itself when it has lagged one or more periods. If the correct ARIMA model is estimated, the Ljung Box statistic tends to be smaller. Conversely, an erroneous model inflates the Ljung Box statistic.